Tree of Thoughts prompting (ToT): Cracking the Code to Simplified Understanding
Unlocking the Next Phase of Generative AI: Exploring the Significance of the Tree of Thoughts Framework with simple to understand example.
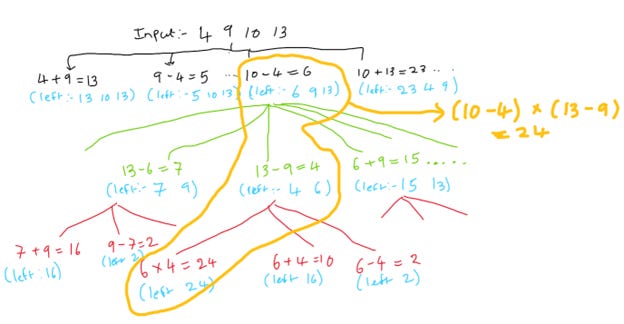
To understand tree of thoughts prompting(ToT), lets try to solve a problem, given 4 digits 4 9 10 13 we need to reach number 24 using a number once and using basic mathematical operation (+-*/) . For e.g. (13–9) * (10–4) = 24
A new course launched for interview preparation
We have launched a new course “Interview Questions and Answers on Large Language Models (LLMs)” series.
This program is designed to bridge the job gap in the global AI industry. It includes 100+ questions and answers from top companies like FAANG and Fortune 500 & 100+ self-assessment questions.
The course offers regular updates, self-assessment questions, community support, and a comprehensive curriculum covering everything from Prompt Engineering and basics of LLM to Supervised Fine-Tuning (SFT) LLM, Deployment, Hallucination, Evaluation, and Agents etc.
Understand detailed curriculum below (Get 50% off using coupon code MED50 for first 10 users)
You can try our FREE self assessment on LLM (30 MCQs in 30 mins)
Lets try to solve this problem using LLM in 4 different ways:
Method 1 : Standard prompt
Lets try few shot prompt with a solution and hope that model can figure out an solution for us, we can use below prompt
standard_prompt = f'''Use numbers and basic arithmetic operations (+ - * /) to obtain 24
Input: 4 4 6 8
Answer: (4 + 8) * (6 - 4) = 24
Input: 2 9 10 12
Answer: 2 * 12 * (10 - 9) = 24
Input: 4 9 10 13
Answer: (13 - 9) * (10 - 4) = 24
Input: 1 4 8 8
Answer: (8 / 4 + 1) * 8 = 24
Input: 5 5 5 9
Answer: 5 + 5 + 5 + 9 = 24
Input: {user_input}
'''If we input number 1 1 2 12 we get below answer
Answer: (12 / 2) * (1 + 1) = 24We know that this is obviously wrong answer as this will result in number 12 while solution could be (12 * 2 * 1 * 1) = 24
Method 2: Few-Shot CoT
Let’s try to provide intermediate steps to a LM and hope that LM can produce accurate intermediate steps and reach to final solution. We can use a prompt like below
# 5-shot
cot_prompt = f'''Use numbers and basic arithmetic operations (+ - * /) to obtain 24. Each step, you are only allowed to choose two of the remaining numbers to obtain a new number.
Input: 4 4 6 8
Steps:
4 + 8 = 12 (left: 4 6 12)
6 - 4 = 2 (left: 2 12)
2 * 12 = 24 (left: 24)
Answer: (6 - 4) * (4 + 8) = 24
Input: 2 9 10 12
Steps:
12 * 2 = 24 (left: 9 10 24)
10 - 9 = 1 (left: 1 24)
24 * 1 = 24 (left: 24)
Answer: (12 * 2) * (10 - 9) = 24
Input: 4 9 10 13
Steps:
13 - 10 = 3 (left: 3 4 9)
9 - 3 = 6 (left: 4 6)
4 * 6 = 24 (left: 24)
Answer: 4 * (9 - (13 - 10)) = 24
Input: 1 4 8 8
Steps:
8 / 4 = 2 (left: 1 2 8)
1 + 2 = 3 (left: 3 8)
3 * 8 = 24 (left: 24)
Answer: (1 + 8 / 4) * 8 = 24
Input: 5 5 5 9
Steps:
5 + 5 = 10 (left: 5 9 10)
10 + 5 = 15 (left: 9 15)
15 + 9 = 24 (left: 24)
Answer: ((5 + 5) + 5) + 9 = 24
Input: {user_input}
'''If we look into section of the prompt below
Input: 4 4 6
Steps:
4 + 8 = 12 (left: 4 6 12)
6 - 4 = 2 (left: 2 12)
2 * 12 = 24 (left: 24)
Answer: (6 - 4) * (4 + 8) = 248We first take 2 numbers and do a arithmetic operation, for e.g. 4 + 8 and then we left with 2 numbers 4 6 and sum of 4 + 8 = 12. So we left with 4 6 12. We follow this steps until we reach a final number.
If we run this prompt for input 1 1 2 12 with temperature set to 0, we get below solution.
Steps:
1 + 1 = 2 (left: 2 12 2)
2 * 2 = 4 (left: 4 12)
4 * 12 = 48 (left: 48)
Answer: (1 + 1) * 2 * 12 = 48Method 3 : Self consistency
The idea is very simple, we generate 100 different outputs using above prompt and use majority vote as final answer, for simplicity we used temperature 0.7 and generated 10 results.
For this use case, what we have seen is that while final answer is printed correct the intermediate steps are incorrect. One such examples is shown below
Steps:
1 + 1 = 2 (left: 2 12 2)
2 * 2 = 4 (left: 4 12)
12 / 4 = 3 (left: 3)
Answer: ((1 + 1) * 2) * (12 / 4) = 24There are couple of reasons why:
The tokens are generated in parallel, final answer is not dependent on intermediate steps.
LMs makes token-level decisions one by one and in a left-to-right fashion.
They refer this method as fast, automatic, unconscious mode (“System 1”).
Although in our example we were lucky to get a final answer of 24 but we know that intermediate steps are incorrect for such method.
Method 4: Tree of thoughts
Let’s look into a diagram on how, we as a human solve this problem using a systematic way. Generally, they referred as slow, deliberate, conscious mode (“System 2”).
We can solve this in 3 steps:
Step 1 : Take 2 numbers and apply all the arithmetic operation at the first level for e.g. 4 + 9 = 13 — sum of first 2 numbers
Step 2 : Identify left numbers as we need to use each number once. Once first 2 numbers are used we left with (left 13 10 13)
Step 3 : Continue to build the tree till we receive final sum.
We can now easily back-track the tree to find final answer with intermediate steps as show in yellow highlighted color.
Practically we can use ToTs in similar way, refer below diagram from the original paper

We use 2 prompts to build a tree
Propose prompt — This prompt will be used to generate first depth of the tree (black color in Fig 1) this will list out all the possible solutions at first level.
Value Prompt — We then can use another few-shot prompt for rest of the depths (green and red in Fig 2) and ask LLMs to evaluate if 24 is possible or not.
To finally evaluate a answer, I use an analogy of toys:
Imagine you have a bunch of toys, and you want to decide which one is the best. When you “value” the toys, you think about each toy and decide how good or how useful it is. You might give each toy a score from 1 to 10, or you might say if it’s really good, just okay, or not good at all.
But sometimes, it’s hard to decide which toy is the best just by looking at them. So instead, you can ask your friends to help you “vote” for the best toy. You show them all the toys and ask them to pick the one they think is the best. Then, you count the votes and see which toy got the most votes. That toy is the winner!
So, “value” is when you decide how good something is by thinking about it, and “vote” is when you ask other people to help you choose the best thing by picking their favorite. This will totally depend on the problem you are solving.
Propose Prompt can be written to get list of first depth answers as below
propose_prompt = f'''Input: 2 8 8 14
Possible next steps:
2 + 8 = 10 (left: 8 10 14)
8 / 2 = 4 (left: 4 8 14)
14 + 2 = 16 (left: 8 8 16)
2 * 8 = 16 (left: 8 14 16)
8 - 2 = 6 (left: 6 8 14)
14 - 8 = 6 (left: 2 6 8)
14 / 2 = 7 (left: 7 8 8)
14 - 2 = 12 (left: 8 8 12)
Input: {user_input}
Possible next steps:
'''We can get below answer
3 + 8 = 11 (left: 11 11)
11 - 8 = 3 (left: 3 11 11)
3 * 8 = 24 (left: 11 11 24)
11 - 3 = 8 (left: 8 11 11)
11 - 8 = 3 (left: 3 11 11)
3 * 11 = 33 (left: 8 11 33)
11 / 3 = 3 (left: 3 8 11)
11 + 3 = 14 (left: 8 11 14)
3 + 8 = 11 (left: 11 11)
8 - 3 = 5 (left: 5 11 11)
11 - 8 = 3 (left: 3 8 11)
11 - 3 = 8 (left: 8 8 11)
3 * 8 = 24 (left: 11 24)
11 + 8 = 19 (left: 3 11 19)
11 / 3 = 3.6666666666666665 (left: 3.67 8 11)
8 / 3 = 2.6666666666666665 (left: 2.67 11 11)
3 + 8 = 11 (left: 11 11)
8 - 3 = 5 (left: 5 11 11)
11 - 8 = 3 (left: 3 8 11)
11 - 3 = 8 (left: 8 8 11)
3 * 8 = 24 (left: 11 24)
11 + 8 = 19 (left: 3 11 19)
11 / 3 = 3.67 (left: 3.67 8 11)
8 / 3 = 2.67 (left: 2.67 11 11)
3 + 8 = 11 (left: 11 11)
8 - 3 = 5 (left: 5 11 11)
11 - 8 = 3 (left: 3 8 11)
11 - 3 = 8 (left: 8 8 11)
3 * 8 = 24 (left: 11 24)
8 / 3 = 2 (left: 2 8 11)
11 + 3 = 14 (left: 8 11 14)
11 / 3 = 3 (left: 3 8 11)
3 + 8 = 11 (left: 11 11)
8 - 3 = 5 (left: 5 11 11)
11 - 8 = 3 (left: 3 8 11)
11 - 3 = 8 (left: 8 8 11)
3 * 8 = 24 (left: 11 24)
11 + 3 = 14 (left: 8 11 14)
11 + 8 = 19 (left: 3 11 19)
8 / 3 = 2 (left: 2 11 11)Value Prompt: To evaluate rest of the depth, we can write below prompt:
value_prompt = f'''Evaluate if given numbers can reach 24 (sure/likely/impossible)
10 14
10 + 14 = 24
sure
11 12
11 + 12 = 23
12 - 11 = 1
11 * 12 = 132
11 / 12 = 0.91
impossible
4 4 10
4 + 4 + 10 = 8 + 10 = 18
4 * 10 - 4 = 40 - 4 = 36
(10 - 4) * 4 = 6 * 4 = 24
sure
4 9 11
9 + 11 + 4 = 20 + 4 = 24
sure
5 7 8
5 + 7 + 8 = 12 + 8 = 20
(8 - 5) * 7 = 3 * 7 = 21
I cannot obtain 24 now, but numbers are within a reasonable range
likely
5 6 6
5 + 6 + 6 = 17
(6 - 5) * 6 = 1 * 6 = 6
I cannot obtain 24 now, but numbers are within a reasonable range
likely
10 10 11
10 + 10 + 11 = 31
(11 - 10) * 10 = 10
10 10 10 are all too big
impossible
1 3 3
1 * 3 * 3 = 9
(1 + 3) * 3 = 12
1 3 3 are all too small
impossible
{no}
'''We get results like below:
Input 11 + 3 = 14 (left: 8 11 14)
Answer: 8 + 11 + 14 = 33
(14–11) * 8 = 24
likely’
Inference: We can infer that 11 + 3 is 14, so (11–11 + 3) * 8 = 24 is one of the solutions.
Input 11–3 = 8 (left: 8 8 11)
Answer: ‘8 + 8 + 11 = 27
(11–8) * 8 = 24
sure’
Inference: We can infer that 11–3 is 8, so (11–3) * (11–8) = 24 is another solution.
For other task and benchmarking on the dataset, refer the original paper
Leave your comments, share and subscribe.



This article comes at such a perfect time, I was just diving deeper into advanced prompting techniques. The Tree of Thoughts explanation with the puzzle is so clear! I'm curious if the new course also explores how to evaluate the quality of these complex reasoning chains beyond just the final answer. Amazing work, realy insightful.